面壁者罗辑希望在宇宙中标记出一个星球。

不过罗辑不能以地球为原点发送坐标，因为这会暴露地球位置。一条咒语由若干组坐标组成，当罗辑选定一个目标星球后，他将再选定几个其他的星球，（可能有重复）,以选定的星球为原点构建坐标系，分别确定出目标星球的坐标，作为咒语的一部分。一个咒语是有效的，当且仅当这条咒语标记出的目标星球只有一个（也就是不会有同时两个星球满足这个咒语的标记）。

作为咒语研究所的一员，你不需要去标定星球，你只需要在咒语发出前判断这条咒语是否有效。罗辑的计划能否成功就取决于你了。

一共有 n 个星球，你已经有一个以地球为原点的星图，上面包括了这 n 个星球，罗辑还会发给你 m 条咒语，每条咒语有 k 组坐标，代表以选定的 k 个星球为原点的目标星球的坐标 为了简化题目，你可以把宇宙想象成二维的，也就是说，所有的坐标都是二维的。

第一行一个整数 n，接下来 n 行每行两个整数，第 i+1 行是编号为 i 的星球的坐标;

接下来一个整数 m，表示 m 条咒语;

接下来 m 行，每行第一个数为 k，接下来 k 组整数x_i , y_i 为以某个星球建立坐标系中的目标星球的坐标。

输出 m 行，对于第 i 行，如果第 i 条咒语不能标记唯一的一个星球，输出“ No solution.”（不含双引号），否则输出那个星球的编号。

【样例解释】

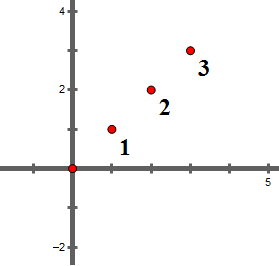
如图，对于第一条咒语，当目标星球为 1 时，1 对于 2 的坐标为 (-1,-1)，1对于3的坐标为(-2,-2)，所以1可以确定是目标星球。

对于第二条咒语，没有任何一个星球与另一个星球的相对坐标为(3,3)，所以无解。

【数据范围】

对于30%的数据：n,m \leq 100，坐标的绝对值 \leq 100;

对于100%的数据：n \leq 2000,m \leq 2000,k的和小于等于3000，坐标的绝对值 \leq 2000;

保证没有两个星球坐标相同。

2017中山市第九届小学生信息学竞赛试题 T4

二维数组