3028 - 圣诞树
众所周知,3202 年的圣诞节快要到了,因此小 Ω 买了一棵圣诞树和一根挂满了彩灯的电线,并打算把这根电线缠绕在圣诞树上。
圣诞树可以视作一个二维平面上有 n 个顶点的凸多边形。这 n 个顶点可以用于固定电线,且按逆时针顺序依次编号为 1, \cdots, n。其中第 i 个顶点的坐标为 (x_i, y_i),记其中 y 坐标最大的顶点的编号为 k(若有多个满足条件的顶点,则取编号最小的)。不保证编号为 1 的顶点的 x 坐标最小。
下图左侧展示了一棵圣诞树的轮廓,其中 y 坐标最大的顶点的编号为 k = 5。

小 Ω 希望用挂满了彩灯的电线装饰这棵圣诞树。出于美观性考虑,她希望这根电线经过所有顶点恰好一次;为了连接电源,这根电线需要从 (x_k, y_k) 出发。形式化地,她需要决定一个 1, \cdots, n 的排列 p_1, \cdots, p_n,满足 p_1 = k,随后这根电线从 (x p1,yp1) 出发,依次经过 (xp2, yp2), \cdots, (xpn, ypn) 。此时,电线长度为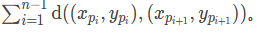
- 其中 \operatorname{d} 为平面上的欧几里得距离,即 \operatorname{d}((x, y), (x', y')) = \sqrt{(x - x')^2 + (y - y')^2}。
上图右侧展示了一种可能的方案,此时对应的排列为 5, 4, 8, 6, 3, 9, 1, 7, 2。
为了节省成本,她希望你能在所有可能的方案中,给出一种使电线长度最短的方案。如果使电线长度最短的方案不唯一,你只需要求出其中任意一种。
考虑到浮点数产生的误差,你输出的方案与最优方案的线段长度的相对误差或绝对误差不超过 10^{-10} 时即认为答案正确。
第一行包含一个正整数 n,表示圣诞树的顶点数。
接下来 n 行,其中第 i 行包含两个精确到小数点后 9 位的实数 x_i, y_i 表示编号为 i 的顶点的坐标。
数据保证这 n 个点两两不同,并且依次连接 (x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n) 将形成一个凸多边形。
输出一行包含 n 个由单个空格隔开的正整数 p_1, p_2, \cdots, p_n,表示一个 1, \cdots, n 的排列,满足 p_1 ,且电线的长度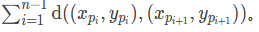
在所有可能的方案中最短。如果这样的方案不唯一,请输出其中任意一种方案。
输入
3 0.000000000 0.000000000 3.000000000 0.000000000 1.000000000 1.000000000
输出
3 1 2
【样例 1 解释】
这一样例中只有下图所示的两种方案,对应排列分别为 3, 1, 2 或 3, 2, 1,电线长度分别为 3 + \sqrt{2} 和 3 + \sqrt{5},而 3 + \sqrt{2} < 3 + \sqrt{5}。
因此答案对应的排列为 3, 1, 2。

【数据范围】
对于所有数据,保证 3 \le n \le 1000;|x_i|, |y_i| \le 10^7。
| 测试点编号 | n \le | 特殊性质 |
|---|---|---|
| 1, 2 | 4 | 无 |
| 3, 4, 5, 6 | 9 | 无 |
| 7, 8, 9, 10, 11, 12 | 18 | 无 |
| 13, 14 | 10^3 | A |
| 15, 16 | 10^3 | B |
| 17, 18, 19, 20 | 10^3 | 无 |
特殊性质 A:保证存在正整数 m \ge n,使得输入的 n 个顶点对应正 m 边形中连续的一段顶点。
特殊性质 B:保证 x_1 < x_2 < \cdots < x_n,且 y_1 > y_2 > \cdots > y_n。
23年NOI春季测试
