3027 - 密码锁
寒假过后,小 I 回到学校,发现自己忘记了自行车锁的密码,于是请你帮忙。
小 I 自行车上的密码锁有 n 个拨圈,每个拨圈有 k(k \leq 4)格。密码锁上的每一格都包含一个正整数,其中第 j 个拨圈的第 i 格上的正整数为 a _ {i, j}。

(一个锁的例子,其中 k = n = 3,每列表示一个拨圈,拨圈的格子从上往下编号。)
你可以对每个拨圈拨若干次(也可以不拨),每拨一次拨圈,它的格子就会进行一次轮换。形式化地,拨第 j 个拨圈一次,则会让第 j 个拨圈上第 i 格的数字移动到第 ((i \bmod k) + 1) 格,其他拨圈不动。
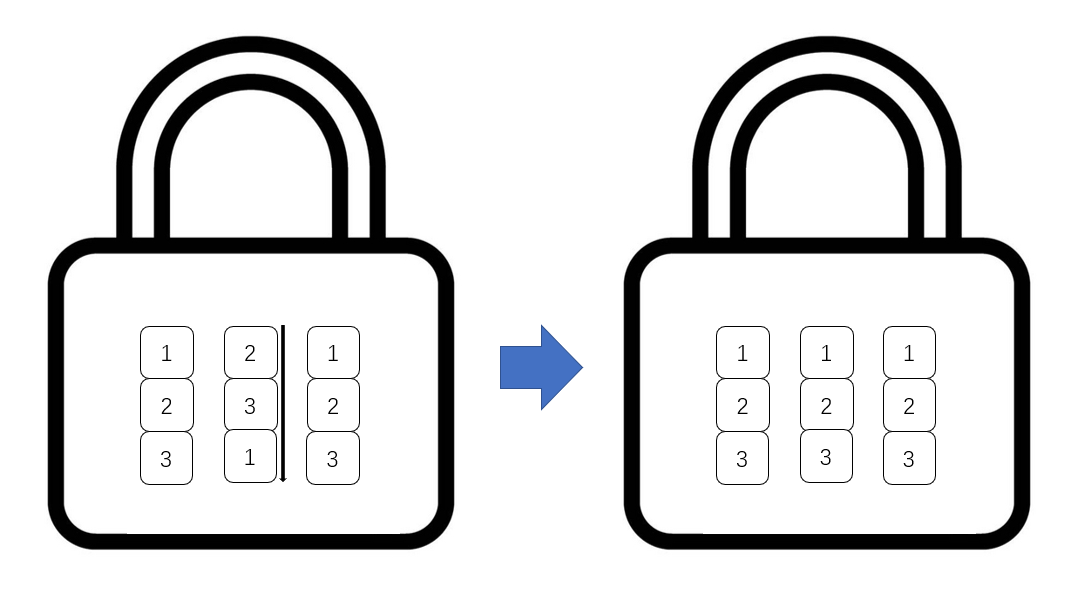
(一个拨动拨圈的例子,对左侧的锁拨一次第二个拨圈得到右侧的锁。)
为了方便记忆,小 I 设定密码时要求同一行上的数字尽可能靠近。 形式化地,对于 1 \leq i \leq k,定义密码锁第 i 行的松散度为
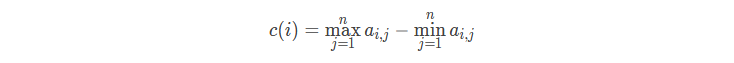
同时定义整个密码锁的松散度为
C = \max \limits _ {1 \leq i \leq k} c(i)
因为能开锁的状态满足 C 尽可能小,因此小 I 希望你找出最小的 C 值。
本题有多组测试数据,题目保证一个测试点中所有测试数据的 k 相同。
第一行包含两个正整数 T, k,分别表示测试数据组数和密码锁拨圈上的格数。
接下来一共 T 组数据,每组数据格式如下:
第一行包含一个正整数 n,表示拨圈数。
接下来 k 行,每行包含 n 个正整数,其中第 i 行第 j 个整数 a _ {i,j} 表示密码锁第 j 个拨圈上第 i 格对应的数字。
注意输入的矩阵中每一列对应一个拨圈,而非每一行对应一个拨圈。
对于每组数据,输出一行包含一个整数,表示所有方案中 C 的最小值。
输入
2 3 3 1 2 1 2 3 2 3 1 3 2 1 2 2 1 1 2
输出
0 1
【样例 1 解释】
第一组样例对应题目描述中的例子。 在拨第二个拨圈一次后,每个拨圈都是 {1, 2, 3},此时松散度为 0。 容易证明无论如何松散度都不可能小于 0,因此输出 0。
以下四个样例分别对应 k = 1, 2, 3, 4 的情况,且样例中 n 的取值有一定梯度。
【数据范围】
设 \sum n 为一个测试点中所有测试数据的 n 的和。
对于所有数据,保证 1 \leq T,1 \leq k \leq 4,1 \leq a _ {i ,j} \leq 3 \times 10 ^ 4。
本题分为两类测试点。
第一类测试点共有十二个,保证 k \leq 3,n \leq 5 \times 10 ^ 4,\sum n \leq 1.5 \times 10 ^ 5。
| 测试点编号 | n \leq | \sum n \leq | k = |
|---|---|---|---|
| 1 | 20 | 100 | 1 |
| 2 | 5 \times 10 ^ 4 | 1.5 \times 10 ^ 5 | 1 |
| 3 | 20 | 100 | 2 |
| 4 | 100 | 1000 | 2 |
| 5 | 2000 | 10 ^ 4 | 2 |
| 6 | 5 \times 10 ^ 4 | 1.5 \times 10 ^ 5 | 2 |
| 7 | 10 | 50 | 3 |
| 8 | 50 | 500 | 3 |
| 9 | 300 | 3000 | 3 |
| 10 | 3000 | 2 \times 10 ^ 4 | 3 |
| 11 | 3 \times 10 ^ 4 | 1.2 \times 10 ^ 5 | 3 |
| 12 | 5 \times 10 ^ 4 | 1.5 \times 10 ^ 5 | 3 |
第二类测试点共有八个,保证 k = 4,n \leq 10 ^ 4, \sum n \leq 3 \times 10 ^ 4。
| 测试点编号 | n \leq | \sum n \leq | k = |
|---|---|---|---|
| 13 | 10 | 50 | 4 |
| 14 | 50 | 500 | 4 |
| 15 | 200 | 2000 | 4 |
| 16 | 500 | 4000 | 4 |
| 17 | 2500 | 10 ^ 4 | 4 |
| 18 | 5000 | 2 \times 10 ^ 4 | 4 |
| 19 | 10 ^ 4 | 3 \times 10 ^ 4 | 4 |
| 20 | 10 ^ 4 | 3 \times 10 ^ 4 | 4 |
23年NOI春季测试
