C. 寻宝冒险
在一个神秘岛屿上, 据说隐藏着一座传说中的宝藏。这座宝藏被认为是无比珍贵的,引来了众多冒险家的追逐。
主人公是一位名叫亚历克斯的年轻冒险家。他听说了这个宝藏的传闻,决定踏上寻宝之旅。但是,为了到达宝藏所在的地点,他必须穿越一片险恶的迷宫。
迷宫由一个 m \times n 矩阵 grid 表示,矩阵的每个单元格都有一个唯一的整数值,代表着该位置的特定路径。亚历克斯只能从每一行的单元格移动到下一行的某个单元格,每次移动都需要支付一定的代价。
老智者告诉他,要找到最小的路径代价,他需要将路径上经过的单元格的值之和,与移动的代价之和相加。
移动的代价用一个下标从 0 开始的二维数组 cost 表示,该数组大小为 (m \times n) \times n ,其中 cost[i][j] 代表值为 i 的单元格移动到下一行第 j 列 (j = 0,1,2...n-1)单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。
grid 一条路径的代价是:所有路径经过的单元格的值之和,加上所有移动的代价之和 。
求从第一行任意单元格出发,到达最后一行任意单元格的最小路径代价。
现在,你有机会像亚历克斯一样,踏上寻宝冒险。通过计算路径的代价,找到通往宝藏的最小路径代价吧!
第一行是 grid 的行数 m、列数 n。
接下来输入 m \times n 个不相同的数值 ( 0 \sim m \times n - 1)。
接下来输入 (m \times n) \times n 个数值表示移动代价, cost[i][j] 代表从值为 i 的单元格移动到下一行第 j 列(j = 0,1,2...n-1)单元格的代价。
最小路径代价。
输入
3 2 5 3 4 0 2 1 9 8 1 5 10 12 18 6 2 4 14 3
输出
17
输入
2 3 5 1 2 4 0 3 12 10 15 20 23 8 21 7 1 8 1 13 9 10 25 5 3 2
输出
6
输入
2 2 0 1 2 3 100 100 1 2 1 1 1 1
输出
4
【样例 1 说明】
样例 1 对应的矩阵如下图所示:
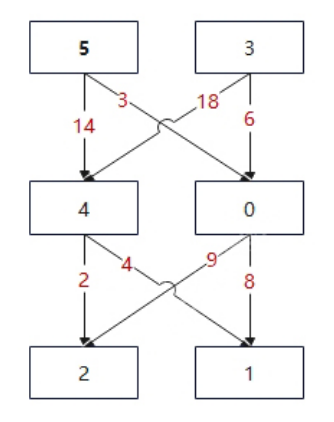
行数为 3,列数为 2。
grid 矩阵为:
5 3
4 0
2 1
cost 数组为:
9 8
1 5
10 12
18 6
2 4
14 3
cost[0][0]=9、cost[0][1]=8,分别代表:数值 0 移动到下一行 j=0 的列代价为 9、移动到下一行 j=1 的列代价为 8。
最小代价的路径是 5 -> 0 -> 1 。
路径途经单元格值之和 5 + 0 + 1 = 6 。
从 5 移动到 0 的代价为 3 。
从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。
【样例 2 说明】
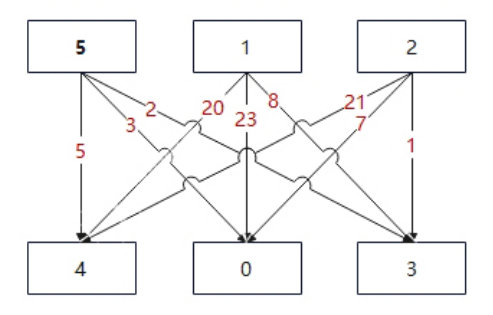
最小代价的路径是 2 -> 3 。
路径途经单元格值之和 2 + 3 = 5 。
从 2 移动到 3 的代价为 1 。
路径总代价为 5 + 1 = 6 。
【样例 3 说明】
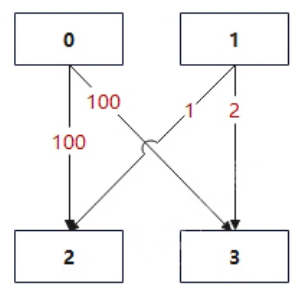
最小代价的路径是 1 -> 2 。
途经最小总代价为 1 + 1 + 2 = 4 。
【数据范围】
对于 100\% 的数据满足:
2 \le m,n \le 50。
0 \le grid[i][j] \le m \times n - 1 ,数值互不相同。
1 \le cost[i][j] \le 100。
| 时间限制 | 1 秒 |
| 内存限制 | 128 MB |
| 提交次数 | 265 |
| 通过人数 | 124 |
| 金币数量 | 0 枚 |
| 难度 | 基础 |