3906 - 美丽路径
题目描述
小杨有一棵包含 n 个节点的树,节点从 1 到 n 编号,并且每个节点要么是白色,要么是黑色。
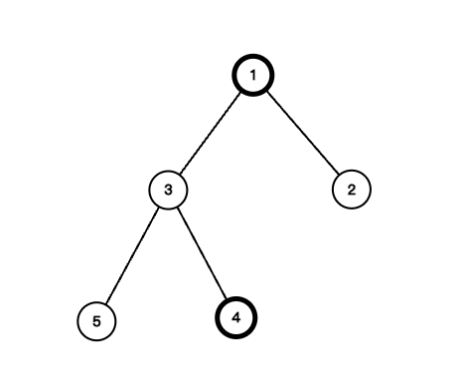
对于树上的一条简单路径(不经过重复节点的路径),小杨认为它是美丽的当且仅当路径上相邻节点的颜色均不相同。例如下图,其中节点 1 和节点 4 是黑色,其余节点是白色,路径2-1-3-4 是美丽路径,而 路径 2-1-3-5 不是美丽路径(相邻节点 3 和 5 颜色相同)。
对于树上的一条简单路径,小杨认为它的长度是路径包含节点的数量。小杨想知道最长的美丽路径的长度是多少。
输入
第一行包含一个正整数 n,代表节点数量。
第二行包含 n 个整数 c_1 , c_2 , \dots , c_n,代表每个节点的颜色,如果 c_i=0,代表节点 i 为白色,如果 c_i=1,代表节点 i 为黑色。
之后 n-1 行,每行包含两个正整数 u_i,v_i,代表存在一条连接节点 u_i 和节点 v_i 的边。
输出
输出一个整数,代表最长美丽路径的长度。
样例
输入
5 1 0 0 1 0 1 2 3 5 4 3 1 3
输出
4
输入
5 0 0 0 0 0 1 2 2 3 3 4 4 5
输出
1
说明
【数据范围】
对于全部数据,保证有 1 \le n \le 10^5,0 \le c_i \le 1 ,同时保证给出的数据构成一棵树。
| 子任务编号 | 数据点占比 | n | 特殊条件 |
|---|---|---|---|
| 1 | 30\% | \le 1000 | 树的形态是一条链 |
| 2 | 30\% | \le 1000 | |
| 3 | 40\% | \le 10^5 |
来源
GESP 9月认证 C++ 八级真题
标签
