2760 - 消息传递
题目描述
A 市的平面图是一个 n \times m 的矩阵。
某日,市长请位于 (1,a) 处的 2 名邮递员,分别向位于 (n,b) 和 (n,c) 处的两所学校传递信息。
矩阵中每个点有一个数字 R ij 代表了邮递员如果走这个点需要支付的费用。请注意,费用的计算包含起点和终点。
两位快递员可以一起先走一段公共的路径,这段公共的路径上,两个快递员只需要支付一份路费。然后两位快递员在某个点 Pij 处分道扬镳,分别向自己的目标位置移动。
请编程计算出,两位快递员从出发点将消息传递到目标点,最少需要支付多少钱的路费。
输入
第一行,读入五个整数 n,m,a,b,c。(0< a,b,c \le m),含义如题目所述。
以下 n 行,每行 m 个整数,表示经过该点需要支付的费用。
输出
输出一个整数,表示答案。
样例
输入
5 5 1 2 4 1 8 1 6 6 1 1 1 2 4 8 3 1 2 2 1 2 1 9 1 1 0 9 1 1
输出
15
说明
样例解释
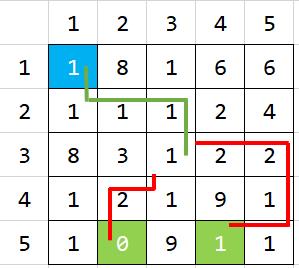
从 (1,1) 点出发,分别走到 (5,2)、(5,4) 点。
先经过绿色的公共路径,需要支付的金额=1+1+1+1+1=5,再分别经过两条红色的路径到达终点,需要支付的金额=(1+2+0)+(2+2+1+1+1)=10,因此总共需要支付的最小金额=15。
数据范围与约定
对于 20\% 的数据,R ij=1,且 b=c(除了20\%,其余数据点均满足 b≠c )。
对于 40\% 的数据,R ij=1,且 b≠c。
对于 100\% 的数据:0 < n,m \le 1000,0 \le R_{i,j}\le 10^9,0< a,b,c \le m 。
标签
