2189 - 医院设置
题目描述
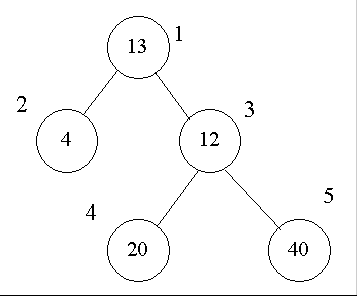
设有一棵二叉树(如图,其中圈中的数字表示结点中居民的人口,圈边上数字表示结点编号。
现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻结点之间的距离为 1 。就本图而言,若医院建在 1 处,则距离和=4+12+2 \times 20+2 \times 40=136;若医院建在 3 处,则距离和=4 \times 2+13+20+40=81……
输入
输入第一行一个整数 n ,表示树的结点数(n≤100)。
接下来的 n 行每行描述了一个结点的状况,包含三个整数,整数之间用空格(一个或多个)分隔,其中:第一个数为居民人口数;第二个数为左链接,为 0 表示无链接;第三个数为右链接,为 0 表示无链接。
输出
输出一个整数,表示最小距离和。
样例
输入
5 13 2 3 4 0 0 12 4 5 20 0 0 40 0 0
输出
81
说明
数据规模也不大,采用邻接矩阵存储,用Floyed法求出任意两结点之间的最短路径长,然后穷举医院可能建立的n个结点位置
来源
树
标签
