南北两岸的猴子们为了香蕉贸易的顺畅，在两岸分别修建了 n 个码头用于船只运送香蕉。规定南岸码头必须运输到北岸相同编号的码头。但是随着码头的不断增加，运送线路存在相汇的情况，大大增加了船只碰撞的风险，如下图所示：

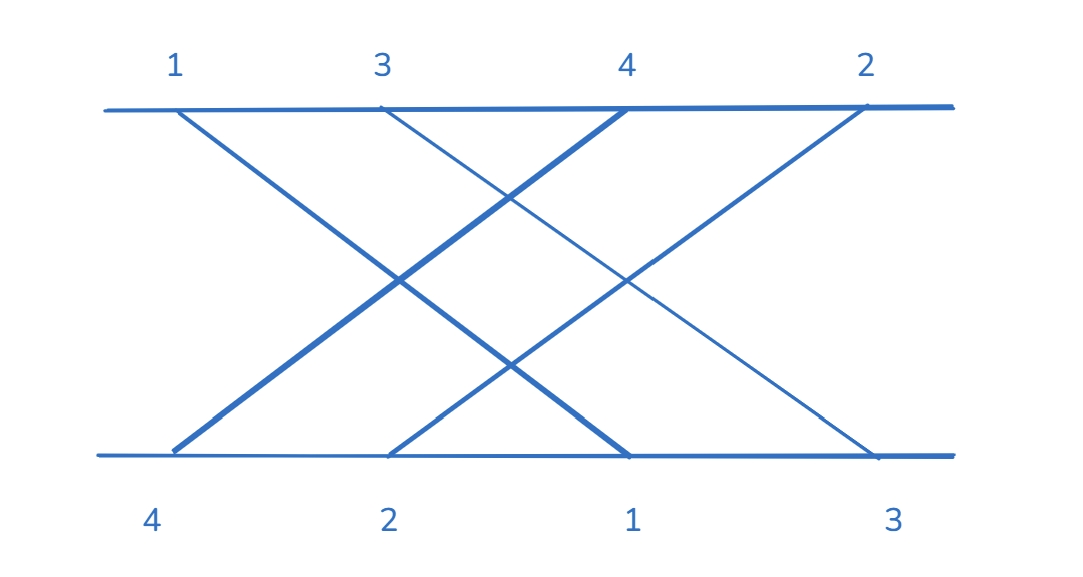
所以猴子们商量着要调整码头的位置，但是调整必须十分小心，所以每次只能调整南岸或者北岸相邻的两个码头的位置， 那么最少需要进行多少次调整，才能让运送线路不存在交叉的情况？

第一行为一个整数 n，表示南北岸分别拥有的码头数量。

第二行为 n 个整数，表示南岸每个码头的编号。

第三行为 n 个整数，表示北岸每个码头的编号。

南岸和北岸码头的编号均在 [1, n] 的范围内，且互不相等。

输出一个整数，表示最少的调整次数。

【样例 1 解释】

最少需要 4 次调整，可以按如下方案调整北岸的码头：

第一步：4 1 2 3。

第二步：4 1 3 2。

第三步：1 4 3 2。

第四步：1 3 4 2。

此时和南岸的码头顺序一致，不会有交叉路线了。

【数据规模】

对于 30 \% 的数据， 1 \leq n \leq 1000。

对于 60 \% 的数据， 1 \leq n \leq 10000。

对于 100 \% 的数据， 1 \leq n \leq 100000。

月赛逆序对分治树状数组