3272 - 水上乐园
暑期到了,小明和朋友们来到了本地有名的水上乐园消暑纳凉。
乐园建在一个宽为 M 高为 N 的矩阵中。矩阵中每个单位的方格中都有一定高度的流水。水会从高向低流淌,大家就可以先沿着方格之间的小路爬到某个较高的位置,然后戴上游泳圈跳入方格,让自己从高向低轻松流淌到四方向相邻的格子中较低水位的方格,好不惬意。
需要注意的是,在四方向相邻的同一个水位的不同方格之间,人们也可以轻松的把自己从一个方格划到另一个方格中,但无法将自己划到比当前方格水位更高的相邻的格子中。
大家在乐园中,一旦到了某个低水位的方格,想要回高水位的方格,就只能从水里出来,沿着方格之间小路爬到高水位的方格位置。
小明觉得,每次要沿小路向上爬实在是太累了。如果能建造几台缆车,将人们从某个低水位的方格送到高水位的方格,一定会受欢迎。于是他把这个想法告诉了乐园经理,经理也觉得是个极好的主意,但预算有限,建造一条缆车价格不菲。
为了最大化缆车的利用价值,经理提出了一个问题:如果每条缆车可以从任意的方格出发,将人们送到其他位置的任意方格(中途不停车下客),那么最少要建造多少条缆车,才能让人们在矩形乐园中不用沿着方格之间的小路走,就可以从任意的方格,到达其他任意的方格呢?
即:只能通过坐缆车,或者在水中从某水位的方格划到四方向相邻格子中,水位不高于当前水位的方格,这两种形式,实现从乐园的任何方格到达另一个任何方格的目标。
第 1 行输入两个整数 M 和 N。
接下来 N 行,每行输入 M 个整数,代表每个方格中水位的高度。
输出要实现题目的目标,最少要建造缆车的数量。
输入
9 3 1 1 1 2 2 2 1 1 1 1 3 1 2 3 2 1 2 1 1 1 1 2 2 2 1 1 1
输出
3
输入
5 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
输出
0
输入
10 4 7 1 1 1 1 1 1 7 7 7 1 3 6 1 9 9 1 7 8 7 1 4 5 1 9 9 1 7 8 7 7 1 1 1 1 1 1 7 7 7
输出
5
样例 1 解释
乐园的平面图如下,如图所示,需要建造 3 条缆车,就可以实现题目要求的目标。
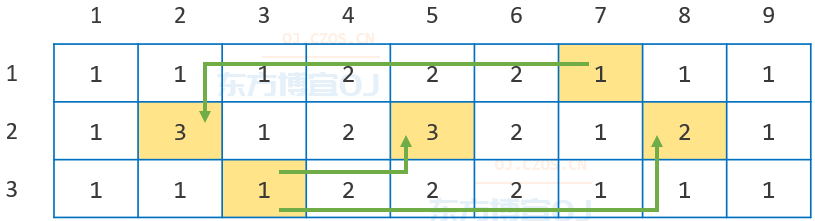
数据范围
对于 50\% 的数据,1 \le M,N \le 50。
对于 100\% 的数据 1 \le M,N \le 500,每个方格水位的高度均在 [1,2000] 之间。
